fitting.dispgauss

fitting.dispgauss(x, A, B, x0, dx)

A single dispersive Gaussian without baseline / offset.

Parameters:
  • x (array) – x-values.
  • A (float) – Amplitude of real part.
  • B (float) – Amplitude of dispersive part.
  • x0 (float) – Center.
  • dx (float) – FWHM.
Returns: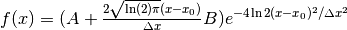

f(x) = (A + \frac{2 \sqrt{\ln(2) \pi} (x - x_0)}{\Delta x} B) e^{-4 \ln 2 (x - x_0)^2 / \Delta x^2}.

Note

This dispersive Gaussian is defined in an analogous manner as the dispersive Lorentzian displor() with an extra factor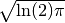 \sqrt{\ln(2) \pi}, which makes the total area under the dispersive and real parts identical.

See also

See Hoffman et al., J. Phys. Chem. A 118, 4955 (2014) on how to use dispersive Lorentzians for analysis of dispersive lineshapes in FSRS.